两种机器人动力学库学习记录
【简介】
最近研究mpc+wbc算法时,需要求解足式机器人的全身动力学模型。目前主流的是使用Pinocchio,但曾经研究过一阵子足式机器人的控制框架mc_rtc,玩过CNRS-AIST JRL实验写的动力学库,于是将趁此机会对两者做一个比较进行学习。
RBDyn 是一个功能强大的 C++ 库,专注于机器人运动学和动力学算法的实现。它支持 C++11 标准,并利用 Eigen3 和 SpaceVecAlg 库提供高效的数学运算支持,其搭配tasks库使用可以轻松实现多刚体模型的各种操作(例如实现足式机器人对质心轨迹、摆动腿轨迹的跟踪等等,其实际上一个基于权重分层WBC的库,后面有时间再进行整理)。该库经过了广泛的测试,并成功应用在HRP-4和Atlas等机器人中。关于它的教程很简单,只有官方提供了在线的 Doxygen 文档以及源码中的test文件,很方便开发者查阅。
Pinocchio是用于刚体动力学建模和控制的开源库。由法国国家计算机与自动化研究所和巴黎索邦大学机器人研究所支持和维护。它提供了一组工具和算法,用于计算机器人的运动学和动力学特性,包括正向和逆向动力学计算、雅可比矩阵计算、惯性矩阵计算等。Pinocchio是一个灵活且高效的库,可用于实现机器人动力学建模、仿真和控制算法的开发。
线上课程ppt及视频:
RBDyn
(1)导入urdf
RBDyn有几种导入机器人呢方式,最简单的需要两个参数,一个为urdf路径,一个ParserParameters结构体,其用于定义相关参数,例如基座是否固定,根节点是哪个等等。
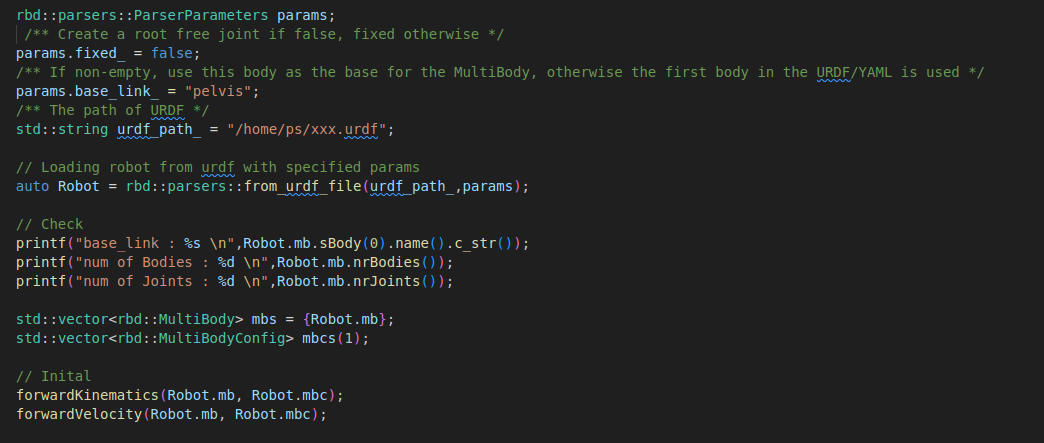
(2)创建求解器
RBDyn是一个动力学库,Tasks是与之配套约束优化控制库,两者进行搭配,可以很方便对多自由度刚体进行控制。这里尝试移动机器人使用comTask移动质心以及positionTasks移动某个body。
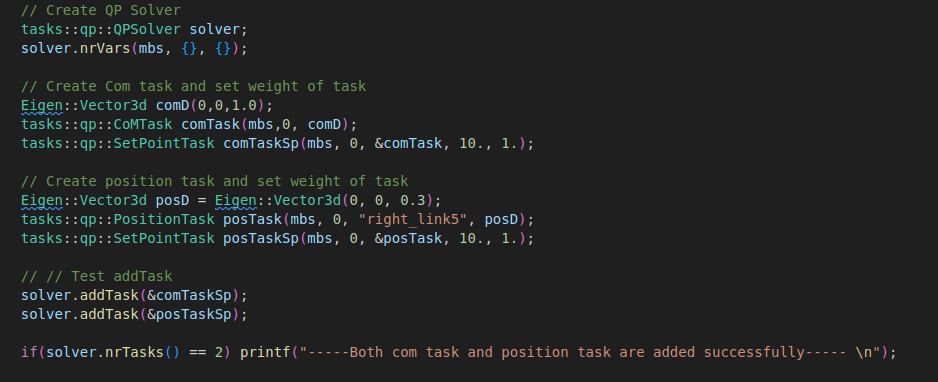
注意:在创建QP求解器时,需要设定qp问题变量的数量和类型,否则求解不成功。这里只用了nrVars函数设定机器人的关节优化变量,其他变量都为零。
(3)计算
调用solve函数对优化问题进行求解,然后进行积分步进,并调用前向运动学更新机器人的姿态。
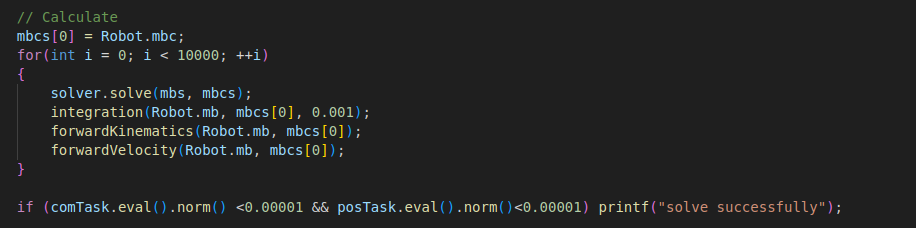
(4)编译
对c++源码也挺简单,直接连接其生成的两个库文件即可(还有一个是task库的)
g++ dynamictest.cpp -o dynamictest_RBDyn -lRBDyn -lRBDynParsers -lTasks注意:由于网络原因,git该库的时候有时无法下载对应cmake文件,需要自己单独下载。
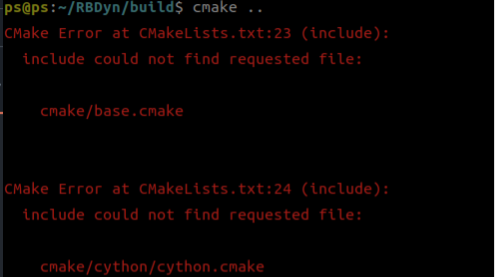
Pinocchio
【导入】
pinocchio有三种导入方式,其中前两者最常用,后两者不推荐使用。
在第二种方法中,floating base的q是7维,前3个是世界坐标系下的坐标向量,后4个是世界坐标系下四元数 (x,y,z,w),v是6维向量,分别是在local坐标系中表示的速度和角速度,加速度a同理。
第三种方法中,floating base的q是6维,即3个平动自由度和3个转动自由度。注意ocs2中pinochio接口使用的是该种方式进行机器人的创建。
std::string urdf_path ="the/path/to/your/urdf";
// 法一:不含浮动基
pinocchio::urdf::buildModel(urdf_path, model);
data = pinocchio::Data(model);
// 法二:含浮动基,nq = dof + 7 ,nv = dof + 6
pinocchio::JointModelFreeFlyer root_joint;
pinocchio::urdf::buildModel(urdf_path, root_joint, model);
data = pinocchio::Data(model);
// 法三:含浮动基,nq = dof + 6 ,nv = dof + 6
pinocchio::JointModelComposite jointComposite(2); // 添加两个关节
jointComposite.addJoint(pinocchio::JointModelTranslation()); // 添加平动3个自由度
jointComposite.addJoint(pinocchio::JointModelSphericalZYX()); // 添加旋转3个自由度
pinocchio::urdf::buildModel(urdf_path, jointComposite, model);
data = pinocchio::Data(model);
【Cheat Sheet】
import pinocchio as pin
# 补
joint.placement/frame.placement # 表示在其父关节坐标系下的变换(SE3 变换矩阵),不会随机器人姿态变化而变化
# Spatial quantities
# 1.Transforms
M = pin.SE3(1) or pin.SE3.Identity() # 单位变化
M.rotation # 旋转矩阵
M.translation # 平移向量
aMb = pin.SE3(aRb, apb)# 创建一个从坐标系b到坐标系a的变换矩阵
pin.SE3.Random() # 生成一个随机的变换矩阵
bMa = aMb.inverse()# 计算变换矩阵的逆
aMc = aMb * bMc # 变换矩阵的乘法
aXb = aMb.action # 变换矩阵对空间向量的作用
aHb = aMb.homogeneous # 获取齐次变换矩阵
pin.log(M) # 将SE3变换矩阵转换为6D向量(对数映射)
pin.exp(M) # 将6D向量转换为SE3变换矩阵(指数映射)
# Data
data = pin.Data(model) 或 data = model.createData() # 创建与模型相关的数据结构
data.joints # 关节数据
data.oMi[jid] # 关节jid在世界坐标系中的变化(SE3变换矩阵),随机器人姿态变化而变化
data.oMf[fid] # 坐标系fid在世界坐标系中的变化(SE3变换矩阵),随机器人姿态变化而变化
data.v # 关节速度
data.a # 关节加速度
data.f # 关节力
data.M # 质量矩阵
data.nle # 非线性效应
data.hg # 质心动量
data.Ag # 质心矩阵
data.Ig # 质心惯性
# Model
model = pin.Model() # 创建机器人模型的运动学树
model.name # 模型名称
model.names # 关节名称
model.joints # 关节模型
model.placements # 关节相对位置,不会随机器人姿态变化而变化
model.inertias # 连杆惯性
model.frames # 获取某个坐标系
model.nq # 位置变量的数量
model.nv # 速度变量的数量
# 输出所有关节
for joint_id in range(robot.model.njoints):
joint_name = robot.model.names[joint_id]
print(f"Joint ID: {joint_id}, Name: {joint_name}")
# 输出所有坐标系
for frame_id in range(robot.model.nframes):
frame_name = robot.model.frames[frame_id].name
print(f"Frame ID: {frame_id}, Name: {frame_name}")
# 返回 q0 to q1的速度向量(注意,输出的是的向量大小为nv,nq中四元数会单独处理)
pinocchio::difference(model_, x1.head(nq), x2.head(nq), dx.head(nv));【正运动学】
// -------- 注意:以下为伪代码 --------
// 1)根据dof设置对应的关节角度q
q<< 0, 0, 0, 1.57, .. , dof;
// 2)调用正运动学函数,将命令q输入,并将结果保存在data中
forwardKinematics(model, data , q)
// 3)获取末端关节索引(注意x的大小,x需要自己定义,使该索引值指向机器人的末端)
JointIndex end_effector_id = model.njoints - x
// 4)通过data结构体与末端索引获取末端位姿
// position
Eigen::Vector3d position = data.oMi[end_effector_id].translation();
// position为列向量,将其转置后更方便输出
std::cout<< position.transpose()<<std::endl;
// Rotation
Eigen::Quaternion quaternion = data.oMi[end_effector_id].rotation();
// 将旋转矩阵转化为四元数后,输出更容易检查
std::cout<< quaternion.coeffs().transpose() <<std::endl;
// 5)可以使用rviz进行显示,并通过tf来检验两者之间的变换
rosrun tf tf_echo /base_link /end_effector_link
【逆运动学】
在逆运动学中,我们核心是计算出各个关节误差v,利用公式 来逐步计算出关节角。已知机械臂微分运动学末端速度旋量等于雅可比矩阵乘以关节角速度,即 ,移项 ,也就是说我们想求各个关节角度微分,必须得求出雅可比矩阵J的逆以及末端速度。但是由于雅可比矩阵不总是可逆,因此在求解时,我们要对雅可比矩阵进行修正与转化。
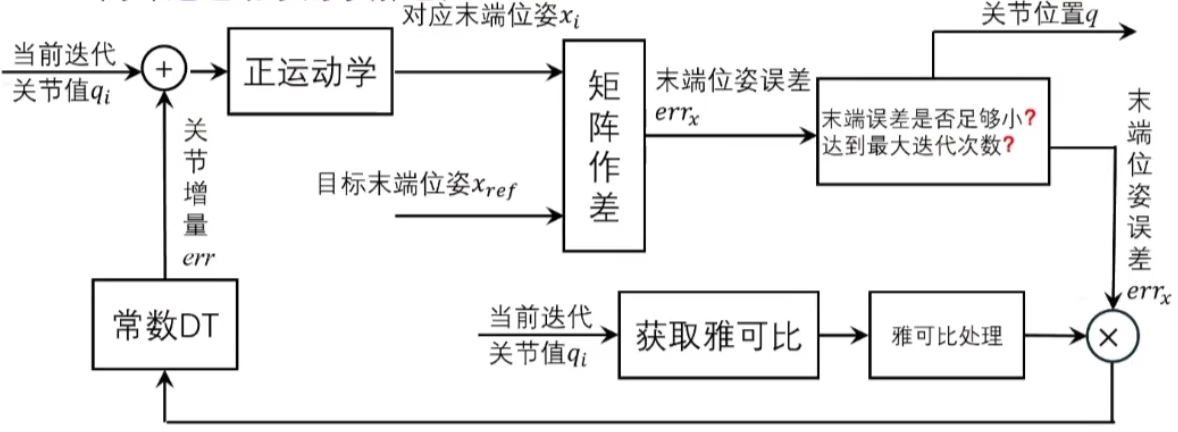
// -------- 注意:以下为伪代码 --------
// 1)设置迭代相关的参数
const double eps = 1e-4;
const int IT_MAX = 100;
const double DT = 6e-1;
const double damp = 1e-2;
// 2)设置目标位姿(相对于世界坐标系)
// 法一:设置一个目标
Eigen::Vector3d desRotation_eul = {0, 0, 0};// 为了方便,可以先设置欧拉角,调用函数将其转化为旋转矩阵
Eigen::Matrix3d desRotation = eul2Rot(desRotation_eul(0), desRotation_eul(1), desRotation_eul(2));
Eigen::Vector3d desPosition = {0, 0, -0.4};
const pinocchio::SE3 target(desRotation, desPosition);// 目标姿态得用SE3数据类型
// 法二:设置多个目标
std::vector<pinocchio::SE3> targets {pinocchio::SE3(Eigen::Quaternion(x,x,x,x),Eigen::Vector3d(x,x,x)), ...}
// 4)开始利用雅可比进行迭代
int itr_count{0};
for (itr_count = 0;; itr_count++)
{
// 5)正运动学更新,数据存储在data中(注意,第一次运行该命令之后模型才真正被初始化!)
pinocchio::forwardKinematics(model, data , q)
// 6)通过末端关节索引以及目标姿态,调用函数计算误差矩阵
// oMi表示某关节在全局坐标系下的变换矩阵
// oMi[xx].actInv(xxx)目标在当前坐标系下的矩阵
const pinocchio::SE3 iMd = data.oMi[end_effector_id].actInv(target);
// 7)将误差矩阵转化为行向量,方便后续计算与输出
errL = pinocchio::log6(iMd).toVector(); // in joint frame
std::cout<<"err大小为"<<err<<std::endl;
// 8)判断是否满足精度,若满足则退出
if (err.norm() < eps) // 满足精度后退出
{
success = true;
break;
}
if (itr_count >= IT_MAX)
{
success = false;
break;
}
// 9)根据当前关节角q,获取雅可比矩阵矩阵J
pinocchio::computeJointJacobian(model, data, q, end_effector_id, J);
std::cout<<"J的大小为"<<J<<std::endl;
// 10)计算了李代数形式的雅可比矩阵的对数,然后获取修正后的雅可比矩阵J
pinocchio::Data::Matrix6 Jlog;
pinocchio::Jlog6(iMd.inverse(), Jlog);
std::cout << "Jlog的大小为"<< Jlog << std::endl;
J = -Jlog * J
Eigen::Matrix<double, 6, 6> JJt; // 注意维度,其与雅可比矩阵维度对应
JJt.noalias() = J * W * J.transpose(); // 这里可以通过一个权益矩阵w,来选择哪些关节不参与逆运动学的计算
// 11)在JJt的对角线加上了阻尼项 damp,以确保矩阵可逆
JJt.diagonal().array() += damp;
// 12)通过求解线性方程组JJt * v = - J^T * err,计算关节误差,
v.noalias() = -W * J.transpose() * JJt.ldlt().solve(err);
std::cout << "v的大小为"<< v << std::endl;
// 13)求解关节增量,并获取最终关节角的值
q = pinocchio::integrate(model, q, v * DT);
std::cout << "q的大小为"<< q << std::endl;
}
【编译】
g++ -std=c++11 overview-simple.cpp -o overview-simple $(pkg-config --cflags --libs pinocchio)【注意事项】
1.当以urdf以固定支座传入时,world坐标系即urdf中第一个joint的坐标系
pinocchio::urdf::buildModel(urdf_path, model);
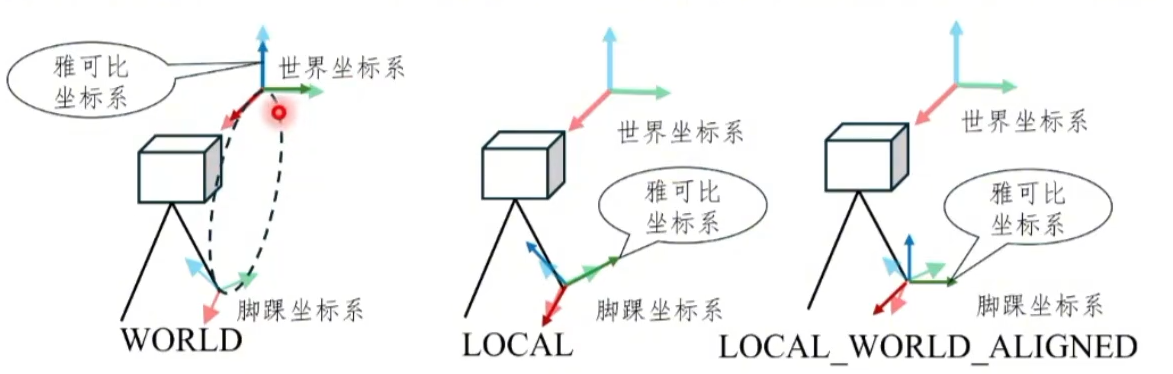
2.Pinocchio中有三种坐标形式,对应下图中的WORLD、LOCAL、LOCAL_WORLD_ALIGNED。(注意:若想获取某个坐标系的速度应该采用第三种方式)
① WORLD:坐标系朝向与世界坐标系平行,原点位于机身最初的base处。
② LOCAL:坐标系与雅可比求解的末端坐标重合。
③ LOCAL_WORLD_ALIGNED:坐标原点在末端坐标原点,但方向与世界坐标系同相。
【参考资料】
4.Openloong开源社区首期线下技术分享会(上)_哔哩哔哩_bilibili
常见的机器人动力学模型库
机器人动力学建模常见的两种基础方法,拉格朗日动力学(基于能量(动能和势能)的建模方法,适用于多自由度系统,如机械臂和移动机器人)和牛顿-欧拉法(基于牛顿力学和欧拉旋转方程,适合递归计算机器人关节的力和力矩)。
所谓的机器人动力学模型库,就是提供了一系列的函数和工具,用于建立、分析和仿真机器人动力学模型。简单收集和罗列一些常见的库,不一定十分全面,仅供参考!
ROS工具包/Kinematics and Dynamics Library (KDL):
提供了强大的机器人运动学和动力学计算功能。它支持正向/逆向运动学、正向/逆向动力学、轨迹规划等。

MATLAB Robotics System Toolbox
强大无须多言!
MATLAB 机器人系统工具箱提供了丰富的函数和工具,用于创建、仿真和控制机器人。它可以处理各种机器人类型,包括串联机器人、并联机器人、移动机器人等。它支持正向/逆向运动学、正向/逆向动力学、轨迹规划、控制等。使用 MATLAB 的符号计算能力,可以推导复杂的动力学方程。

RBDL (Rigid Body Dynamics Library)
一个高效的 C++ 库,实现了刚体多体系统的正向和逆向动力学算法,如递归牛顿-欧拉算法、复合刚体算法和关节空间惯性矩阵的计算。
据说该库的开发是参照这本书籍《Rigid Body Dynamics Algorithms》

书籍链接:
Robot Dynamics Library (RDL)
基于 RBDL,但更强调运动学处理的正确性,通过运行时检查确保参考系规则得到遵守。
Drake
MIT 开发的工具箱,用于分析和设计机器人系统。包含广泛的动力学和控制算法,并支持多种机器人模型。用 C++ 编写,并提供 Python 接口。专注于鲁棒性和优化。

DART (Dynamic Animation and Robotics Toolkit)
支持刚体和软体动力学,集成了多种碰撞检测器(如 FCL、Bullet 和 ODE),支持正逆动力学计算,C++编写。
Pinocchio
一个快速且高效的机器人运动学和动力学库,用 C++ 编写。专为实时性能而设计,适合用于机器人控制和仿真。支持正向/逆向运动学、正向/逆向动力学、雅可比矩阵计算、重心计算等。与 ROS 兼容。
OpenRAVE
是一个用于机器人运动规划、控制和仿真的开源库。它提供了丰富的动力学模型支持,包括刚体动力学、关节动力学等。可以方便地创建和模拟各种机器人系统,并进行运动规划和控制算法的开发。
支持多种编程语言,如 C++、Python 等,具有良好的跨平台性。
总是有人走在前面,在GitHub中,有人总结了很多知识,总结了很多库,详细的信息如下,
Awesome Robotics Libraries
机器人学习库,这个是一个十分好的项目,重点罗列了很多机器人控制或应用所需的一些机器人开发库文件。比如机器人动力学仿真、运动学求解、机器人建模、优化、轨迹规划和运动控制等等。
同时,在该项目中,还对同类型的机器人库进行了简单的梳理、比较和总结,让我们能够更清楚,更快速选择自己想要的,十分便利。比如一些常见的动力学仿真库,一些常见的特点,编程语言,源码,关注度等等,总结的十分详细而全面,值得学习。

以上就是找到的一些动力学库,仅供参考!
相关文章

